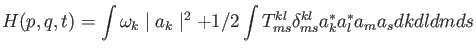Testimonials of preveous students
For the summer I was involved in a research project
involving the study of Fermi-Pasta-Ulam (FPU) beta-chains.
During my time studying under the supervision of Dr. Lvov,
I brushed up on classical Lagrangian and Hamiltonian mechanics,
studied the numerical solutions of non-linear coupled differential equations,
and derived the four-wave kinetic equation amongst other things.
I began my studies by reading a Doctoral Thesis written by Boris Gershgorin.
Before this summer, I had not sat down to read a dissertation and was very
intimidated by the length and thoroughness of the paper. I was asked to derive
the equations of motion from the Hamiltonian, which were in the form of first
order differential equations involving p’s and q’s as the dymanical variables.
I then expressed the Hamiltonian,
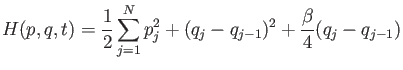 |
|
|
(1) |
in terms of the Fourier conjugates
of p and q, such that
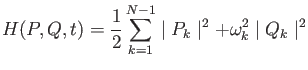 |
|
|
(2) |
![$\displaystyle +\frac{\beta}{4N}
\sum _{k,l,m,s=1} ^{N-1}
\omega _k
\omega _l
\o...
...k
Q_l
Q_m
Q_s^*
\delta _s^{klm}
+c.c.)
+
Q_k
Q_l
Q_m^*
Q_s^*
\delta _{ms}^{kl}]$](img4.png) |
|
|
(3) |
where P and Q are the Fourier conjugates of p
and q respectively. Finally, I was told to express the Hamiltonian in terms of
variables which were still canonical and analogous to the raising and lowering
operators used in quantum mechanics, namely a and a*. So far, I was only required
to confirm the conclusions that Boris Gershgorin came to in his thesis, and ensure
that I understood that math and concepts.
After doing the derivations, which took about ten pages, I began to have a
lot of respect for the amount of time that was put into the dissertation. It
wasn’t until doing those ten pages of derivations that I began to understand
two or three lines in the thesis. The derivation of those equations was useful
because they helped me to review basic Hamiltonian principles, Fourier Transforms,
delta functions, and algebraic concepts such the product of multiple sums. Important
values which were used in the computations were:
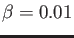 |
|
|
(4) |
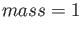 |
|
|
(5) |
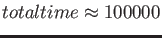 |
|
|
(6) |
It is important to note that the inital conditions of all the momenta and
positions were randomly generated such that the average momentum of all the particles
was zero and that the average position was also zero. Additionally, the initial conditions
were set so that the initial energy was 50. The accuracy of the energy conservation was not the best.
While the initial energy was 50, the ending value of energy was 46.0871. Because of the untilization
of the Runge-Kutta integration method, conservation of Energy was not perfect. Yoshida method
would have worked more nicely.
I also developed a more intuitive understanding of how creation and annihilation
operators corresponded to the creation and annihilation of waves in Fourier space.
Next, I was asked to solve for the equations of motion of a system of
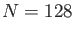 |
|
|
(7) |
particles. I very much appreciated this part of the research project. The study
of non linear FPU chains was most stimulating because, unlike the typical sets of
problems that are introduced in physics courses for studies which are linear and
hence directly integrable, the FPU chains had a non-linear term which makes it
not directly solvable.
The first experience I had with solving a non-linear set of differential equations
was when I chose to solve for equations of motion (EOM) for the double pendulum.
I used the Lagrangian and the Euler-Lagrange equation to find the two second order
differential equations. While I found this to be interesting, I had never given
thought to solving any larger systems. At first, I was completely shocked that
I would have to solve for 256 coupled equations of motion. After brushing up on
MATLAB syntax, I was able to use Runge-Kutta method on the Hamiltonian EOM.
The Runge-Kutta method is a very interesting way to solve coupled differential equations.
Matlab uses RK4-5. A very good text which explains the principles of RK can be found
in "Scientific Computing: An introductory Survey" written by Michael T. Heath.
It was a very enlightening experience. While I had studied basic numerics
in the RPI course on “Numerical Computing,” I had never been required to do
anything as complicated and lengthy as 256 equations. After checking the behavior
of the EOM over large periods of time, I was able to verify that I had written the
program correctly. I found it very interesting when I was asked to plot the p’s
and q’s over a long time span. Each showed quasi-periodic behavior, as expected.
One way that I could verify that the EOM were correct was by checking to see if
certain quantities were being conserved as I expected. Energy and momentum were
nearly conserved. While the energy drifted a bit, I had read in Gershgorin’s
thesis that Yoshida method of integration was often used to make sure this quantity
was conserved better. I found his discourse on Yoshida method interesting but did
not use it. Another way I confirmed that the equations of motion were probably correct
was by giving the system a total center-of-mass initial momentum, and making sure
that the center-of-mass position moved with accordance to what I would expect from
classical mechanics. The results were canonical.
During this project, I took the liberty of reading about the history of FPU
chains and was interested to learn about what is called the FPU paradox. It is said
that non-linear systems are not directly solvable and so they have to be solved
using numerical methods. These systems are said to exhibit chaotic motion, as I
understand. However, during one of the experiments that was run by Fermi, Ulam,
Pasta and Tsingou, the experiment was run for a longer period of time than intended,
and it was discovered that the system returned, after a long period of time, to a
state that was similar to the initial conditions. This seemed troubling because
non-linear systems are supposed to exhibit chaotic motion, and clearly there was
a long period quasi-periodic quality about this system. As it turns out, the more
“directly integrable” a problem is, the less chaotic its behavior will appear.
The less integrable the EOM are, the more ergodic their behavior is. If the system
is very non-linear, then it is expected that the system become very chaotic as
time progresses, and that thermalization and equipartition of energy would take
place.
Understanding to what degree of nonlinearity a system needs to be in order
to reach thermalization is something that I wish to have a better understanding
of.
Next, I was asked to derive the four-wave kinetic equation. I derived both
the three- and four-wave kinetic equations using Gershgorin’s thesis, and a book
by Dr. Victor Lvov named Kolmogorov Spectra of Turbulence as guides. Starting
with the three- and four-wave interaction Hamiltonian, I derived the three- and
four-wave kinetic equation after much algebraic manipulation. While this process
was difficult and I had to rely heavily on the sources that I was given, I was
able to complete the derivation, exercising time dependent perturbation theory,
basic complex variables, statistics and Dirac delta functions. The Hamiltonian for the four-wave interactions was:
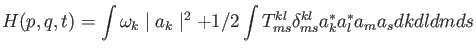 |
|
|
(8) |
Lastly, I was required to show the relation between nk and wk. I did this
by starting with the Bose-Einstein statistics for an ensemble of indistinguishable
bosons. The Bose-Einstein statistics, as I learned from Thermodynamics and
Statistical Mechanics class, is the energy distribution on indistinguishable
particles in thermal equilibrium. Since this system is in the classical limit,
I was able to make the assumption that
 |
|
|
(9) |
Because of this, I was able to
prove that
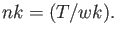 |
|
|
(10) |
Upon proving this, it became my task to take the system of 128 particles above,
and let the system evolve over a long period of time, and check to see if thermal
equilibrium was reached. Since (6) was the criterion for thermal equilibrium
in the classical regime, it made since that if I plotted
 |
|
|
(11) |
versus
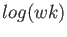 |
|
|
(12) |
I should be able to see and near linear relationship. This is precisely what I did. (See Figure 1).
One question that was left unresolved was the use of the Bose-Einstein statistics.
I was wondering why it was that we didn’t use Maxwell-Boltzmann distribution for the
derivation of (5). After all, MB statistics describe the energy
distribution of distinguishable particles and is a classical paradigm that both FD and
BE statistics go to in the classical limit.
All in all, I had a very rewarding experience this summer studying under Dr.
Lvov. Although a lot was demanded out of me, I was able to refine and apply my
knowledge of classical mechanics, thermodynamics, and statistics and further
develop numerical methods and computing techniques. A research project like
this was the perfect opportunity to exercise my knowledge in mathematics and
physics beyond the classroom.
Dr Yuri V Lvov
2019-08-29
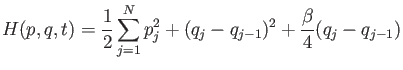
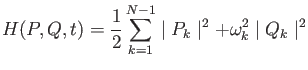
![$\displaystyle +\frac{\beta}{4N}
\sum _{k,l,m,s=1} ^{N-1}
\omega _k
\omega _l
\o...
...k
Q_l
Q_m
Q_s^*
\delta _s^{klm}
+c.c.)
+
Q_k
Q_l
Q_m^*
Q_s^*
\delta _{ms}^{kl}]$](img4.png)