


Next: Hamiltonian Description of Acoustic
Up: Basic equation of motion
Previous: Basic equation of motion
Consider the Euler equations for a compressible fluid:
| |
|
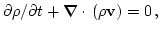 |
|
| |
|
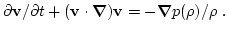 |
(23) |
Here 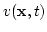 is the Euler fluid velocity,
is the Euler fluid velocity,
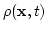 the density, and
the density, and 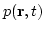 is the pressure which, in the general
case, is a function of fluid density and specific entropy
is the pressure which, in the general
case, is a function of fluid density and specific entropy 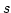 [
[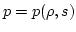 ]. In ideal fluids where there is no viscosity and heat
exchange, the entropy per unit volume is carried by the fluid, i.e.
obeys the equation
]. In ideal fluids where there is no viscosity and heat
exchange, the entropy per unit volume is carried by the fluid, i.e.
obeys the equation
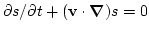 . A fluid in which the specific entropy is
constant throughout the volume is called barotropic; the pressure in
such fluid is a single-valued function of density
. A fluid in which the specific entropy is
constant throughout the volume is called barotropic; the pressure in
such fluid is a single-valued function of density 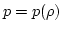 . In
this case,
. In
this case,
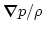 may be expressed via the gradient of
specific enthalpy of unit mass
may be expressed via the gradient of
specific enthalpy of unit mass 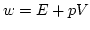 and
and
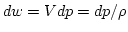 . Thus,
. Thus,
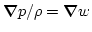 .
.
Writing the fluid density
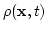 as
as
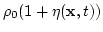 , the velocity field as
, the velocity field as 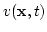 , the pressure field as
, the pressure field as
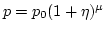 and the enthalpy as
and the enthalpy as
one can write (2.1) to third order in amplitude
in the following form
Let us introduce new variables as
where
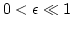 ,
,
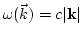 and
and 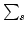 connotes summation over
connotes summation over 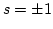 . From
(2.2) and (2.3),
. From
(2.2) and (2.3),
where the summation is done over all signs of
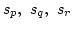 and we
used the shorthand notation
and we
used the shorthand notation
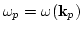 . The coupling
coefficients are,
. The coupling
coefficients are,
These coefficients have the following important properties:
where 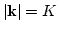 . Note that if
. Note that if
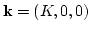 ,
the resonant manifold is not of codimension
one but degenerates to
,
the resonant manifold is not of codimension
one but degenerates to 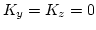 , where
, where
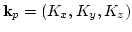 ,
,
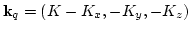 . There are three cases.
. There are three cases.
- For
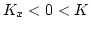 ,
,
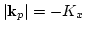 ,
,
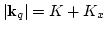 ,
,
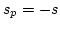 ,
, 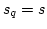 .
.
- For
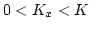 ,
,
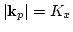 ,
,
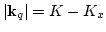
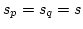 .
.
- For
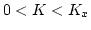 ,
,
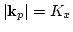 ,
,
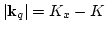 ,
,
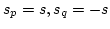 .
.



Next: Hamiltonian Description of Acoustic
Up: Basic equation of motion
Previous: Basic equation of motion
Dr Yuri V Lvov
2007-01-17
![]() as
as
![]() , the velocity field as
, the velocity field as ![]() , the pressure field as
, the pressure field as
![]() and the enthalpy as
and the enthalpy as