


Next: One-pole approximation
Up: Diagrammatic Approach to Acoustic
Previous: Objects of Diagrammatic Technique
In the diagrammatic series for the Green's function one may perform
the partial Dyson's summation over one-particle irreducible
diagrams. This results in the Dyson equation for the Green's functions:
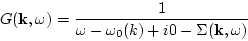 |
(68) |
where the ``mass operator''
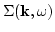 gives the
nonlinear correction to the complex frequency
gives the
nonlinear correction to the complex frequency
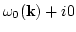 due to the interaction (2.19). This is an infinite series with
respect to the bare amplitude
due to the interaction (2.19). This is an infinite series with
respect to the bare amplitude
 (2.20), dressed Green's function (4.2) and double
correlation function
(2.20), dressed Green's function (4.2) and double
correlation function
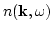 (4.3). All of the
contributions of the second and fourth order in
(4.3). All of the
contributions of the second and fourth order in  are shown on Fig
1(b).
are shown on Fig
1(b).
We have not specified the direction of arrows on Fig 1(b); each
diagram should be interpreted as a sum of diagrams with all possible
directions of arrows compatible with vortex
 , describing the three-wave processes
, describing the three-wave processes
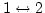 . For
example, diagram (a) on Fig 1(b) corresponds to three diagrams shown
on Fig 2. The diagram (a4) on Fig 2 describes the nonresonant process
. For
example, diagram (a) on Fig 1(b) corresponds to three diagrams shown
on Fig 2. The diagram (a4) on Fig 2 describes the nonresonant process
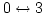 which is not essential for our consideration.
which is not essential for our consideration.
With the help of the similar Dyson's summing of one-particle
irreducible diagrams, one can derive Wyld's equation for
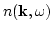 :
:
![\begin{displaymath}
n({\bf k},\omega) = \vert G({\bf k},\omega)\vert^2\left[D({\bf k},\omega
)+\Phi({\bf k},\omega)\right] \ .
\end{displaymath}](img361.png) |
(69) |
Here
 is the correlation function of white noise,
is the correlation function of white noise,
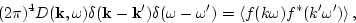 |
(70) |
and the mass operator
 describes the nonlinear
corrections to
describes the nonlinear
corrections to
 . This is an infinite series with
respect to the same objects
. This is an infinite series with
respect to the same objects
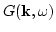 ,
,
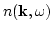 and
and
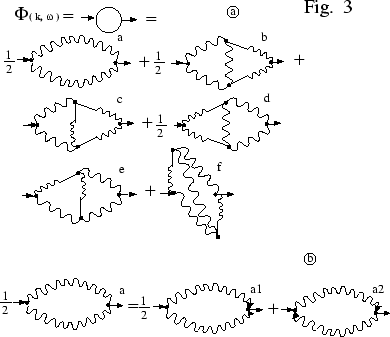
 . All diagrams of the second and
fourth order are shown on Fig 3(a).
. All diagrams of the second and
fourth order are shown on Fig 3(a).
We also have not specified arrow directions in the diagrams for
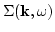 and
and
 . In complete
analogy with diagrams for
. In complete
analogy with diagrams for
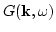 one diagram on Fig 3a
corresponds to two diagrams (a1) and (a2) on Fig 3b. All the
rest diagrams for
one diagram on Fig 3a
corresponds to two diagrams (a1) and (a2) on Fig 3b. All the
rest diagrams for
 reproduces in the same way -
one chooses all possible directions of arrows and discards those which
incompatible with definition of vertex
reproduces in the same way -
one chooses all possible directions of arrows and discards those which
incompatible with definition of vertex  (see Fig 1a).
(see Fig 1a).
Figure 3:
First terms in the diadrammatic pertubation expansion for
mass operator
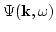 .
.
 |



Next: One-pole approximation
Up: Diagrammatic Approach to Acoustic
Previous: Objects of Diagrammatic Technique
Dr Yuri V Lvov
2007-01-17
![]() , describing the three-wave processes
, describing the three-wave processes
![]() . For
example, diagram (a) on Fig 1(b) corresponds to three diagrams shown
on Fig 2. The diagram (a4) on Fig 2 describes the nonresonant process
. For
example, diagram (a) on Fig 1(b) corresponds to three diagrams shown
on Fig 2. The diagram (a4) on Fig 2 describes the nonresonant process
![]() which is not essential for our consideration.
which is not essential for our consideration.
![]() :
:
![]() and
and
![]() . In complete
analogy with diagrams for
. In complete
analogy with diagrams for
![]() one diagram on Fig 3a
corresponds to two diagrams (a1) and (a2) on Fig 3b. All the
rest diagrams for
one diagram on Fig 3a
corresponds to two diagrams (a1) and (a2) on Fig 3b. All the
rest diagrams for
![]() reproduces in the same way -
one chooses all possible directions of arrows and discards those which
incompatible with definition of vertex
reproduces in the same way -
one chooses all possible directions of arrows and discards those which
incompatible with definition of vertex ![]() (see Fig 1a).
(see Fig 1a).