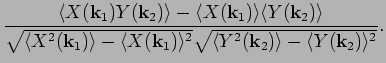Next: Discussions
Up: Results
Previous: Nonlinearly active modes and
WT closure relies on the RPA properties of the wave fields, i.e. that
the amplitudes 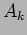 and the phase factors
and the phase factors 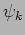 are statistically
independent variables. On the other hand, WT calculation for the
phases
are statistically
independent variables. On the other hand, WT calculation for the
phases 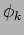 shows that these quantities get correlated. In order
to check these properties and predictions numerically, let us
introduce a function that measures the degree of statistical
dependence (or independence) of some Fourier-space variables
shows that these quantities get correlated. In order
to check these properties and predictions numerically, let us
introduce a function that measures the degree of statistical
dependence (or independence) of some Fourier-space variables
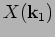 and
and
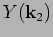 ,
,
For example, we can examine to what degree amplitudes 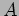 and independent
of the phase factors
and independent
of the phase factors 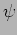 by looking at the function
by looking at the function
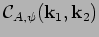 for different values of
for different values of 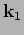 and
and 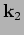 . Independence of the amplitudes at different wavenumbers
can be examined by the auto-correlation function
. Independence of the amplitudes at different wavenumbers
can be examined by the auto-correlation function
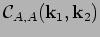 , and similar for the phase factors
and the phases.
We restrict ourselves with choosing
, and similar for the phase factors
and the phases.
We restrict ourselves with choosing
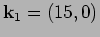 and
and
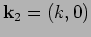 with
with
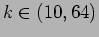 .
Figure 15 shows the values of correlators
.
Figure 15 shows the values of correlators
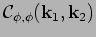 and
and
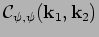 as functions of
as functions of 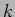 .
In agreement with WT predictions,
auto-correlations of
.
In agreement with WT predictions,
auto-correlations of 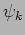 's are very small
whereas
the ones of
's are very small
whereas
the ones of 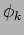 's are significant (except, of course,
for
's are significant (except, of course,
for 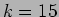 where by definition these correlators are equal to one).
Correlators
where by definition these correlators are equal to one).
Correlators
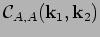 and
and
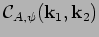 are shown in figure 16. Again, we see a good agreement
with the WT prediction: these correlations are very small (except, again,
are shown in figure 16. Again, we see a good agreement
with the WT prediction: these correlations are very small (except, again,
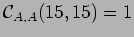 ).
).



Next: Discussions
Up: Results
Previous: Nonlinearly active modes and
Dr Yuri V Lvov
2007-01-16
![]() and the phase factors
and the phase factors ![]() are statistically
independent variables. On the other hand, WT calculation for the
phases
are statistically
independent variables. On the other hand, WT calculation for the
phases ![]() shows that these quantities get correlated. In order
to check these properties and predictions numerically, let us
introduce a function that measures the degree of statistical
dependence (or independence) of some Fourier-space variables
shows that these quantities get correlated. In order
to check these properties and predictions numerically, let us
introduce a function that measures the degree of statistical
dependence (or independence) of some Fourier-space variables
![]() and
and
![]() ,
,