


Next: Frequency properties.
Up: Results
Previous: Spectrum
Now we consider the PDF of amplitudes for which predictions where made
recently within the WT approach. To measure the PDF of amplitudes
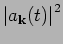 , we set two radial regions in
, we set two radial regions in
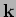 -space
-space
![$ k_{15}=[13,17],$](img174.png) and
and
![$ k_{35}=[33,37]$](img175.png) . These
regions were inside the inertial range and had well mixed phases and
amplitudes since the experiment was done after performing 2000
rotations of the peak mode. We looked at the time-span of
approximately 855 rotations of modes
. These
regions were inside the inertial range and had well mixed phases and
amplitudes since the experiment was done after performing 2000
rotations of the peak mode. We looked at the time-span of
approximately 855 rotations of modes 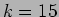 or 1230 rotations of modes
or 1230 rotations of modes
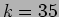 and collected amplitudes of all modes from these three
regions. The number of amplitudes collected was over 1.1 million in
region
and collected amplitudes of all modes from these three
regions. The number of amplitudes collected was over 1.1 million in
region 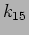 and over 2.1 million in region
and over 2.1 million in region 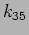 .
.
Figure 4:
Probability density function for
the amplitude 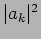 with
with
![$ k \in [33,37]$](img183.png) .
Same notations as in Figure 3.
.
Same notations as in Figure 3.
|
[width=10cm]akpdf35.eps
|
Figure 3 shows a log-plot of the PDF the amplitude 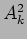 in
in 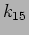 and an exponential fit of its low-amplitude part. One can
see intermittency, i.e., an anomalously large probability of strong
waves. We can also see that this discrepancy from Gaussianity happens
in the tail, i.e. well below the mean amplitude value
and an exponential fit of its low-amplitude part. One can
see intermittency, i.e., an anomalously large probability of strong
waves. We can also see that this discrepancy from Gaussianity happens
in the tail, i.e. well below the mean amplitude value  . While
the PDF tail in not long enough for drawing decisive conclusions about
realization of the theoretically predicted
. While
the PDF tail in not long enough for drawing decisive conclusions about
realization of the theoretically predicted  scaling, it certainly
gives a conclusive evidence that the probabilities of large amplitudes
are orders of magnitude higher than in Gaussian turbulence. Figure
4 shows the PDF of
scaling, it certainly
gives a conclusive evidence that the probabilities of large amplitudes
are orders of magnitude higher than in Gaussian turbulence. Figure
4 shows the PDF of  in
in 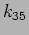 . We can see some
non-Gaussianity in
. We can see some
non-Gaussianity in 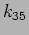 as well, although much less than in
as well, although much less than in
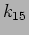 . Similar conclusion that the gravity wave turbulence is more
intermittent at low rather than high wavenumbers was reached on the
basis of numerical simulations in [3].
. Similar conclusion that the gravity wave turbulence is more
intermittent at low rather than high wavenumbers was reached on the
basis of numerical simulations in [3].
Deviations from Gaussianity can be also seen in figure 5
which shows ratio of the moments
 to their values in Gaussian turbulence,
to their values in Gaussian turbulence,  . Again, we can see
that such deviations are greater at the small-
. Again, we can see
that such deviations are greater at the small-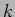 part of the inertial
range.
part of the inertial
range.



Next: Frequency properties.
Up: Results
Previous: Spectrum
Dr Yuri V Lvov
2007-01-16
![]() , we set two radial regions in
, we set two radial regions in
![]() -space
-space
![]() and
and
![]() . These
regions were inside the inertial range and had well mixed phases and
amplitudes since the experiment was done after performing 2000
rotations of the peak mode. We looked at the time-span of
approximately 855 rotations of modes
. These
regions were inside the inertial range and had well mixed phases and
amplitudes since the experiment was done after performing 2000
rotations of the peak mode. We looked at the time-span of
approximately 855 rotations of modes ![]() or 1230 rotations of modes
or 1230 rotations of modes
![]() and collected amplitudes of all modes from these three
regions. The number of amplitudes collected was over 1.1 million in
region
and collected amplitudes of all modes from these three
regions. The number of amplitudes collected was over 1.1 million in
region ![]() and over 2.1 million in region
and over 2.1 million in region ![]() .
.
![]() to their values in Gaussian turbulence,
to their values in Gaussian turbulence, ![]() . Again, we can see
that such deviations are greater at the small-
. Again, we can see
that such deviations are greater at the small-![]() part of the inertial
range.
part of the inertial
range.