


Next: Bibliography
Up: Appendix 2
Previous: Calculation of
Expression for 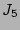 seemingly involves a great number terms.
However, this number can be dramatically reduced by the following
speculation. Just as in
seemingly involves a great number terms.
However, this number can be dramatically reduced by the following
speculation. Just as in  there is no dotted lines in the graphs
involved in
there is no dotted lines in the graphs
involved in 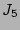 because for each summation index there is a
corresponding wave amplitude present. Thus, we have the same rule for
the number of summations surviving the phase averaging (i.e. one less
than the number of internal couplings). In order to be of the same
order as the leading terms in
because for each summation index there is a
corresponding wave amplitude present. Thus, we have the same rule for
the number of summations surviving the phase averaging (i.e. one less
than the number of internal couplings). In order to be of the same
order as the leading terms in 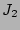 and
and 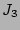 , we must have 3 purely
internal couplings and, therefore, no external couplings. This is only
possible when the number of dotted lines directed to the vertices is
equal to the number of them pointing away which is true for the
, we must have 3 purely
internal couplings and, therefore, no external couplings. This is only
possible when the number of dotted lines directed to the vertices is
equal to the number of them pointing away which is true for the 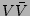 terms but not true for the
terms but not true for the 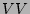 and
and 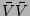 terms. Thus we will only consider the
terms. Thus we will only consider the 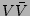 terms. Further, the
fact that there is no external couplings means that such terms are
only non-zero when all
terms. Further, the
fact that there is no external couplings means that such terms are
only non-zero when all  's are zero. Thus, there will be no
contribution from the second part of
's are zero. Thus, there will be no
contribution from the second part of 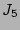 which has a
which has a 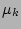 pre-factor.
pre-factor.
where the 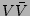 terms to be averaged here are
terms to be averaged here are
By coupling the dashed lines we have in the leading order
Term 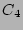 does not survive the averaging because
does not survive the averaging because 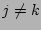 and a
triple internal coupling is not possible. Summarising,
and a
triple internal coupling is not possible. Summarising,
![\begin{displaymath}
J_5= 2 \prod_l\delta(\mu_l) \sum_{j\neq k,n}\lambda_j\lambda...
...elta_{jk}^n\vert^2
\right]
A_j^2 A_n^2 A_k^2 \;\; [1+O(1/N)].
\end{displaymath}](img475.png) |
(81) |



Next: Bibliography
Up: Appendix 2
Previous: Calculation of
Dr Yuri V Lvov
2007-01-17
![$\displaystyle {1 \over 2} \left<\prod_l \psi_l^{(0)\mu_l}
\sum_{j \ne k}\lambda...
...{(0)}+\bar a_j^{(1)}
a_j^{(0)})a_k^{(1)}\bar a_k^{(0)}
\right>_\psi [1+O(1/N)],$](img453.png)

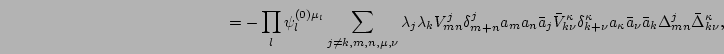

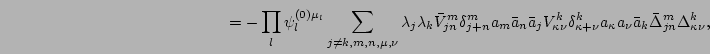

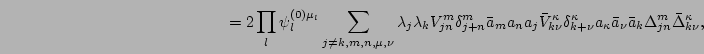

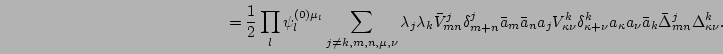

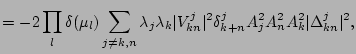

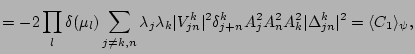

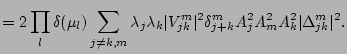
![]() does not survive the averaging because
does not survive the averaging because ![]() and a
triple internal coupling is not possible. Summarising,
and a
triple internal coupling is not possible. Summarising,