


Next: Discussion
Up: Joint statistics of amplitudes
Previous: One-mode statistics
Importantly, RPA formulation involves independent
phase factors 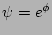 and not phases
and not phases
 themselves. Firstly, the phases
would not be convenient because, as we will see later,
the mean value of the phases is evolving and one could
not say that they are ``distributed uniformly from
themselves. Firstly, the phases
would not be convenient because, as we will see later,
the mean value of the phases is evolving and one could
not say that they are ``distributed uniformly from 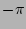 to
to 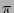 ''. In fact, we will also see that the mean fluctuation
of the phase distribution is also growing and they quickly
spread beyond their initial
''. In fact, we will also see that the mean fluctuation
of the phase distribution is also growing and they quickly
spread beyond their initial 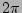 -wide interval.
But perhaps even more important,
-wide interval.
But perhaps even more important,  's build mutual correlations
on the nonlinear
time whereas
's build mutual correlations
on the nonlinear
time whereas 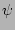 's remain independent.
This will be shown later in this section, but
we would like first to give a simple example
illustrating how this property is possible due
to the fact that correspondence between
's remain independent.
This will be shown later in this section, but
we would like first to give a simple example
illustrating how this property is possible due
to the fact that correspondence between  and
and 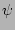 is not a bijection.
is not a bijection.
Let  be a
random integer and let
be a
random integer and let 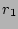 and
and 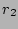 be
two independent (of
be
two independent (of  and of each other)
random numbers with uniform distribution between
and of each other)
random numbers with uniform distribution between 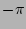 and
and
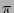 . Let
. Let
Then
and
Thus,
which means that variables  and
and
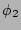 are correlated.
On the other hand, if we introduce
are correlated.
On the other hand, if we introduce
then
and
which means that variables  and
and
 are statistically independent.
In this illustrative example it is clear
that the difference in statistical properties
between
are statistically independent.
In this illustrative example it is clear
that the difference in statistical properties
between  and
and 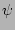 arises from the fact
that function
arises from the fact
that function 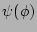 does not have inverse
and, consequently, the information about
does not have inverse
and, consequently, the information about  contained in
contained in  is lost in
is lost in 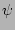 .
.
This illustration, although simple,
captures the property that actually happens in reality
as we will show below.
Let us use the following expression for the
phase
Substituting
(8) and Taylor-expanding of logarithm in  one gets
one gets
 |
|
|
(47) |
where
Now let us perform averaging over the statistics of factors 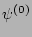 .
As usual, the surviving terms are those in which all
.
As usual, the surviving terms are those in which all 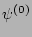 's cancel out
due to their pairwise matchings. This is possible only if the number of
's cancel out
due to their pairwise matchings. This is possible only if the number of 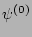 's
is equal to the number of
's
is equal to the number of
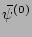 's in the products defining these terms.
Easy to see that the
's in the products defining these terms.
Easy to see that the  term involves three
term involves three 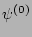 's
and therefore its average is zero. Therefore,
's
and therefore its average is zero. Therefore,
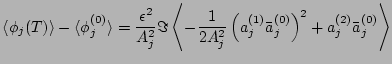 |
|
|
(51) |
Let us consider
Here, there are two terms with equal number of
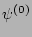 's and
's and
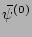 's but all
couplings of index
's but all
couplings of index 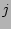 to any other index give
zero because
to any other index give
zero because 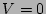 if one of its wavenumbers is zero.
Thus,
if one of its wavenumbers is zero.
Thus,
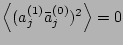 .
The other term,
.
The other term,
 has already been
calculated before when evaluating
has already been
calculated before when evaluating 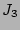 . We have
. We have
Let us take limits
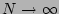 and
and
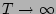 and replace
and replace
 by
by
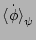 .
We get
.
We get
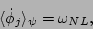 |
(52) |
where 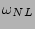 is the nonlinear frequency correction
given by
is the nonlinear frequency correction
given by
![\begin{displaymath}
\omega_{NL}
=
4{\epsilon}^2\int \left[\vert V_{mn}^j\vert^2 ...
...} \right)
\delta_{j+n}^m(A_m^2-A_n^2)\right]A_j^2 \, dk_m dk_n
\end{displaymath}](img344.png) |
(53) |
Here  denotes the principal value of the integral.
Averaging over the amplitudes, we have
denotes the principal value of the integral.
Averaging over the amplitudes, we have
where
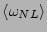 is the amplitude-averaged
nonlinear frequency correction
is the amplitude-averaged
nonlinear frequency correction
![\begin{displaymath}
\langle \omega_{NL} \rangle
=
4{\epsilon}^2\int \left[\vert ...
...n}^m} \right)
\delta_{j+n}^m(n_m-
n_n)\right]n_j \, dk_m dk_n
\end{displaymath}](img348.png) |
(54) |
We can see that the mean value of the phase is steadily changing
over the nonlinear time and, therefore, it would be incorrect to
assume that the phase ``remains uniformly distributed from 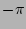 to
to 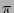 '' even though this could be true for
'' even though this could be true for 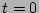 .
This is one of the reasons why we formulate RPA in terms of
.
This is one of the reasons why we formulate RPA in terms of
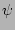 and not
and not  . Indeed,
. Indeed, 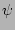 was shown above to stay
uniformly distributed on the unit circle over the nonlinear time.
was shown above to stay
uniformly distributed on the unit circle over the nonlinear time.
The other reason is that, strictly speaking,  's do not
stay de-correlated where as
's do not
stay de-correlated where as 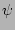 's do (as shown before).
We already saw in the beginning of this section that this
situation is possible due to the fact that the map
's do (as shown before).
We already saw in the beginning of this section that this
situation is possible due to the fact that the map
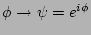 is not a bijection. Let us now
study such a buildup in statistical dependence of the phases,
let us consider correlator
is not a bijection. Let us now
study such a buildup in statistical dependence of the phases,
let us consider correlator
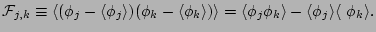 At time
At time  we have
we have
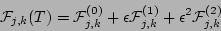 |
(55) |
where
Here, we have taken into account that, as we showed earlier,
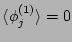 .
Let us consider the
.
Let us consider the  -term
-term
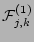 , e.g.
, e.g.
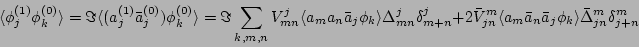 |
(57) |
In this expression, we have a factor 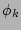 which enters directly and not via the
combination
which enters directly and not via the
combination
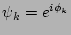 . Potentially, this could greatly complicate the situation
because to objects like
. Potentially, this could greatly complicate the situation
because to objects like
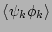 knowledge of the statistics of
knowledge of the statistics of 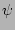 is not sufficient and one needs the full PDF of
is not sufficient and one needs the full PDF of 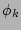 .
Fortunately, however, this does not cause problems here because, no matter what index
is matched to
.
Fortunately, however, this does not cause problems here because, no matter what index
is matched to  , matching of the two remaining indices results in
, matching of the two remaining indices results in 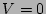 .
Therefore, the contribution of the
.
Therefore, the contribution of the  -terms is nill.
-terms is nill.
Let us now consider the
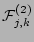 starting with
starting with
![$\displaystyle \langle\phi_j^{(2)}\phi_k^{(0)}\rangle_\psi =
\left<\Im\left[-\fr...
...a_j^{(0)})^2
+\frac{1}{A_j^2}a_j^{(2)}\bar a_j^{(0)}\right]\phi_k^{(0)}\right>.$](img365.png) |
|
|
(58) |
We see that the square bracket on the RHS involves an even number (four or six)
of  in each term. Thus, in order for these terms to survive these
in each term. Thus, in order for these terms to survive these
 must cancel out which is possible when their indices match in a pairwise
way. But this means that index
must cancel out which is possible when their indices match in a pairwise
way. But this means that index  (of
(of 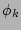 ) does not match to any
of the indices of
) does not match to any
of the indices of  and, therefore, the averaging of
and, therefore, the averaging of 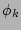 can be taken separately because it is statistically independent of
all other phase factors.5Thus, we conclude that
can be taken separately because it is statistically independent of
all other phase factors.5Thus, we conclude that
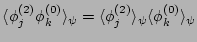 and these terms drop out of
and these terms drop out of
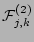 .
The remaining term in
.
The remaining term in
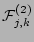 is
is
We can now average over the amplitudes and
take limits 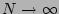 and
and
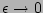 and write
and write
Presence of the 1-st term on the RHS indicates
that the phases of the 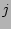 -th and the
-th and the  -th
modes get correlated on the nonlinear time.
This correlation is week in a sense that
-th
modes get correlated on the nonlinear time.
This correlation is week in a sense that
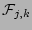 has a sharp peak at
has a sharp peak at 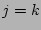 but
the integrated contribution of all
but
the integrated contribution of all 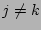 is of the same order as the value at the contribution
of the
is of the same order as the value at the contribution
of the 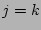 peak and, therefore, could cause a problem
should one tried to build RPA based on the statistics
of
peak and, therefore, could cause a problem
should one tried to build RPA based on the statistics
of  's rather than
's rather than 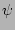 's (which remain de-correlated).
's (which remain de-correlated).
Let us consider a special case of
(61) for 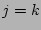 which is interesting because it
allows one to calculate the dispersion in phases,
which is interesting because it
allows one to calculate the dispersion in phases,
We have
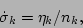 |
(61) |
where 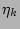 is defined in (44) and
is defined in (44) and
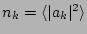 .
One can see that the
RHS here is always positive and, therefore, the phase fluctuations
experience an unlimited growth. On stationary spectra, this
growth is
.
One can see that the
RHS here is always positive and, therefore, the phase fluctuations
experience an unlimited growth. On stationary spectra, this
growth is 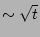 which corresponds to
which corresponds to  .
Recall that the mean value of the phase is also changing in time
with the rate
.
Recall that the mean value of the phase is also changing in time
with the rate 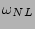 and on stationary spectra this
change is linear in time.
and on stationary spectra this
change is linear in time.



Next: Discussion
Up: Joint statistics of amplitudes
Previous: One-mode statistics
Dr Yuri V Lvov
2007-01-17
![]() be a
random integer and let
be a
random integer and let ![]() and
and ![]() be
two independent (of
be
two independent (of ![]() and of each other)
random numbers with uniform distribution between
and of each other)
random numbers with uniform distribution between ![]() and
and
![]() . Let
. Let

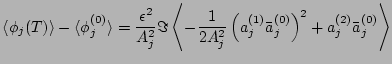
![\begin{displaymath}
\omega_{NL}
=
4{\epsilon}^2\int \left[\vert V_{mn}^j\vert^2 ...
...} \right)
\delta_{j+n}^m(A_m^2-A_n^2)\right]A_j^2 \, dk_m dk_n
\end{displaymath}](img344.png)
![\begin{displaymath}
\langle \omega_{NL} \rangle
=
4{\epsilon}^2\int \left[\vert ...
...n}^m} \right)
\delta_{j+n}^m(n_m-
n_n)\right]n_j \, dk_m dk_n
\end{displaymath}](img348.png)
![]() 's do not
stay de-correlated where as
's do not
stay de-correlated where as ![]() 's do (as shown before).
We already saw in the beginning of this section that this
situation is possible due to the fact that the map
's do (as shown before).
We already saw in the beginning of this section that this
situation is possible due to the fact that the map
![]() is not a bijection. Let us now
study such a buildup in statistical dependence of the phases,
let us consider correlator
is not a bijection. Let us now
study such a buildup in statistical dependence of the phases,
let us consider correlator
![]() At time
At time ![]() we have
we have
![]() starting with
starting with
![$\displaystyle \langle\phi_j^{(2)}\phi_k^{(0)}\rangle_\psi =
\left<\Im\left[-\fr...
...a_j^{(0)})^2
+\frac{1}{A_j^2}a_j^{(2)}\bar a_j^{(0)}\right]\phi_k^{(0)}\right>.$](img365.png)
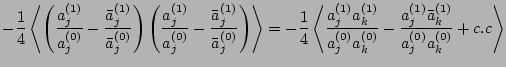
![$\displaystyle {\delta^j_k \over A_{j}^2}
\sum_{l,m}
\left[\vert V_{lm}^{j}\vert...
...{jl}^{m}\vert^2 \vert\Delta_{jl}^{m}\vert^2 \delta_{l+j}^{m}
\right]
A_l^2A_m^2$](img372.png)
![]() which is interesting because it
allows one to calculate the dispersion in phases,
which is interesting because it
allows one to calculate the dispersion in phases,