Yeontaek Choi![]() , Yuri V. Lvov
, Yuri V. Lvov![]() , Sergey Nazarenko
, Sergey Nazarenko![]() and Boris Pokorni
and Boris Pokorni![]()
![]() Mathematics Institute, The University of Warwick, Coventry, CV4-7AL, UK
Mathematics Institute, The University of Warwick, Coventry, CV4-7AL, UK
![]() Department of Mathematical Sciences, Rensselaer Polytechnic Institute,
Troy, NY 12180
Department of Mathematical Sciences, Rensselaer Polytechnic Institute,
Troy, NY 12180
Yeontaek Choi![]() , Yuri V. Lvov
, Yuri V. Lvov![]() , Sergey Nazarenko
, Sergey Nazarenko![]() and Boris Pokorni
and Boris Pokorni![]()
![]() Mathematics Institute, The University of Warwick, Coventry, CV4-7AL, UK
Mathematics Institute, The University of Warwick, Coventry, CV4-7AL, UK
![]() Department of Mathematical Sciences, Rensselaer Polytechnic Institute,
Troy, NY 12180
Department of Mathematical Sciences, Rensselaer Polytechnic Institute,
Troy, NY 12180
Introduction -- Wave Turbulence (WT) is a common name for the fields of dispersive waves which are engaged in stochastic weakly nonlinear interactions over a wide range of scales. Numerous examples of WT are found in oceans, atmospheres, plasmas and Bose-Einstein condensates [1,2,3,4,5,6,7,8,9]. For a long time, describing and predicting the energy spectra was the only concern in WT theory. More recently, some attention was given to the study of turbulence intermittency. WT intermittency, or ``burstiness'' of the turbulent signal, was observed experimentally and numerically and was attributed, as in most turbulent systems, to the presence of coherent structures. Examples include collapsing filaments in Bose-Einstein condensates with attractive potentials [9,10], condensate quasi-solitons in systems with repulsive potentials [9,11,12], white caps of sea waves at small scales [13], freak ocean waves at larger scales [14]. Often, such coherent structures are intense but quite sparse so that in most of the space waves remain weakly nonlinear and mostly unaffected by these structures.
Recent analysis of the higher order cumulants [15] showed that WT becomes strongly non-Gaussian at the same length scale where it fails to be weakly nonlinear. In scale invariant systems, the ratio of nonlinear time to the linear wave period grows as a power-law either in to small or toward large wavenumbers. When this growth coincides with the cascade direction then one expects the WT breakdown if the inertial range is large enough. Otherwise intermittency never occurs provided that turbulence is weak at the forcing scale [16]. Further, even if a significant non-Gaussianity occurs, it does not in itself imply intermittency because PDF may remain, in principle, of the same order as Gaussian in all of its parts. This motivates us to study PDFs in WT. Study of PDF in WT context can be traced back to as early as the work of Pierls [17], and, latter, in [18,19], who considered waves in anharmonic crystals, a special case of 3-wave systems. Recently, equations for multimode and one-mode PDF's where derived and analyzed for the general case of 3-wave systems [21,20]. PDF's of the three wave systems were also studied to explain entropy production in three-wave turbulence systems [22]. In the present paper, we will be concerned with the 4-wave case. We are also motivated by a puzzling numerical evidence of a low-wavenumber intermittency in the system of water-surface gravity waves [23] whereas the analysis of [15] predicts intermittency at high wave numbers only. Explaining this fact could shed light on the phenomenon of freak waves [14].
The idea of the present letter is based on the observation that even if the ``hard'' breakdown (as in [15]) does not occur, there will always be a part of the PDF tail for which the amplitudes are too high for WT to work. Such a ``mild'' breakdown will modify the PDF tail in a way that may correspond to intermittency. In fact, this case is easier to study analytically because WT still works for most of the PDF and the wave breaking phenomenon can be modeled simply as a phenomenological cutoff of the PDF tail reflecting the fact that no waves exist above the breaking amplitude. The wave breaking causes ``leakage'' and, therefore, a flux in the amplitude space which is the key phenomenon leading to deviations from the Gaussian equilibrium and intermittency. Note an analogy with the well-known k-space fluxes (cascades) corresponding to Kolmogorov turbulence which is qualitatively different from the thermodynamic equilibrium state. In this paper we will derive an equation for the wave amplitude PDF and we will find its steady state solutions corresponding to the finite flux in the amplitude space. Consequently, we will show that the resulting wave fields are intermittent at each wavenumber with an anomalously large probability of the large-amplitude waves.
Definition of RPA fields -- Previously, the random phase approximation (RPA) has typically assumed that the phases evolve much more rapidly than the amplitudes and, therefore, there exist time intervals where the phases are random but the amplitudes are deterministic [1]. However, numerical simulations indicate that the phase and the amplitude vary at the same time scale [25]. Thus, we need to generalize RPA to the case where both the phases and the amplitudes are random quantities. Such generalization was done in [20,21,24] where 3-wave systems were considered. In the present letter, we will be dealing with 4-wave systems.
Let us consider a wavefield ![]() in a periodic box of
volume
in a periodic box of
volume ![]() and let the Fourier transform of this field be
and let the Fourier transform of this field be ![]() where
where
![]() and
and ![]() is the space dimension. Later we
take the large box limit in order to consider homogeneous wave
turbulence. Let us write complex
is the space dimension. Later we
take the large box limit in order to consider homogeneous wave
turbulence. Let us write complex ![]() as
as
![]() where
where
![]() is the amplitude and
is the amplitude and
![]() is
a phase factor (
is
a phase factor (![]() being the unit circle in the complex
plane). We say the wavefield
being the unit circle in the complex
plane). We say the wavefield ![]() is of the RPA type if all
variables in the set
is of the RPA type if all
variables in the set
![]() are
statistically independent random variables and
are
statistically independent random variables and ![]() 's are
uniformly distributed on
's are
uniformly distributed on ![]() .
Defined this way RPA refers not only to the phase but also the
amplitude statistics and therefore we suggest a slightly different
reading of this acronym: ``Random Phase and Amplitude''.
.
Defined this way RPA refers not only to the phase but also the
amplitude statistics and therefore we suggest a slightly different
reading of this acronym: ``Random Phase and Amplitude''.
The above properties are sufficient for our WT analysis and yet such
fields may be strongly non-Gaussian. Indeed, RPA allows any shape of
the PDF for amplitudes ![]() and, therefore, it will be a good tool
for describing intermittency.
and, therefore, it will be a good tool
for describing intermittency.
Weakly nonlinear evolution --
Consider a weakly nonlinear wavefield dominated by the 4-wave
interactions, e.g. the water-surface gravity
waves [1,5,7,13], Langmuir waves in
plasmas [1,3] and the waves described by the nonlinear
Schroedinger equation [9]. In the finite box, we have the
following Hamiltonian equations for the Fourier modes of this field,
For small nonlinearity, the linear time-scale
![]() is a
lot less than the nonlinear evolution time which (as will be evident
below, see e.g. (
is a
lot less than the nonlinear evolution time which (as will be evident
below, see e.g. (![]() )) is
)) is
![]() .
Thus, to filter out fast oscillations at the wave period, let us seek
for the solution at an intermediate time
.
Thus, to filter out fast oscillations at the wave period, let us seek
for the solution at an intermediate time ![]() such that
such that
![]() . Now let us use a perturbation
expansion in small
. Now let us use a perturbation
expansion in small ![]() ,
,
![]() Substituting this in (
Substituting this in (![]() ) we get in the
zeroth order a time independent result,
) we get in the
zeroth order a time independent result,
![]() .
For simplicity, we will write
.
For simplicity, we will write ![]() , understanding that a
quantity is taken at
, understanding that a
quantity is taken at ![]() if its time argument is not mentioned
explicitly. The first iteration of (
if its time argument is not mentioned
explicitly. The first iteration of (![]() )
gives
)
gives
Evolution of statistics -- We will now develop a statistical
description via averaging over the initial fields ![]() which are
taken to be of the RPA type. Of course, to have a non-trivial
description valid over the nonlinear evolution time, the fields must
remain of the RPA type over the nonlinear time in the leading order in
which are
taken to be of the RPA type. Of course, to have a non-trivial
description valid over the nonlinear evolution time, the fields must
remain of the RPA type over the nonlinear time in the leading order in
![]() . The proof of this statement in the 3-wave case was
presented in [21,20]. Also [20] contains an
announcement of the 4-wave equation for the multi-mode PDF; the
details of the relevant analysis will be published separately. Let us
introduce a generating function
. The proof of this statement in the 3-wave case was
presented in [21,20]. Also [20] contains an
announcement of the 4-wave equation for the multi-mode PDF; the
details of the relevant analysis will be published separately. Let us
introduce a generating function
![]() where
where ![]() is a real parameter. Then PDF of the wave intensities
is a real parameter. Then PDF of the wave intensities
![]() at each
at each ![]() can be written as an inverse Laplace
transform,
can be written as an inverse Laplace
transform,
![]() For the one-point moments we have
For the one-point moments we have
At ![]() we have
we have
We see from (![]() ) that the choice
) that the choice
We therefore obtain
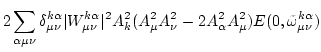 |
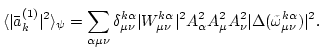 |
To complete the derivation of the equation for the time evolution of
the generating function ![]() we have to take a large box limit,
which implies that sums will be replaced with integrals, the Kronecker
deltas will be replaced with Dirac's deltas,
we have to take a large box limit,
which implies that sums will be replaced with integrals, the Kronecker
deltas will be replaced with Dirac's deltas,
![]() , where we introduced short-hand
notation,
, where we introduced short-hand
notation,
![]() . Then
(
. Then
(![]() ) will still hold, but with
) will still hold, but with
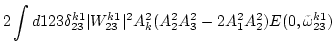 |
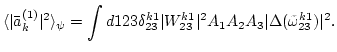 |
| (10) |
Further we take a large ![]() limit, and take into account that
limit, and take into account that
Finally we perform amplitude averaging, noticing that
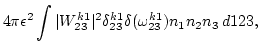 |
|||
![$\displaystyle 8 \pi \epsilon^2 \int \vert W^{k1}_{23}\vert^2 \delta^{k1}_{23}
\delta(\omega^{k3}_{12})
\Big[ n_1 (n_2 + n_3) - n_2 n_3\Big] d123,$](img104.png) |
At the tail of the PDF, ![]() , the solution can be represented
as series in
, the solution can be represented
as series in ![]() ,
,
![]() Thus, the leading order asymptotic of the finite-flux solution is
Thus, the leading order asymptotic of the finite-flux solution is
![]() which describes strong intermittency.
which describes strong intermittency.
Note that if the weakly nonlinearity assumption was valid uniformly to
![]() then we would have to put
then we would have to put ![]() to ensure positivity of
to ensure positivity of ![]() and the convergence of its normalization,
and the convergence of its normalization,
![]() . In this
case
. In this
case
![]() which is a pure Rayleigh
distribution corresponding to the Gaussian wave field. However, WT
approach fails for the amplitudes
which is a pure Rayleigh
distribution corresponding to the Gaussian wave field. However, WT
approach fails for the amplitudes ![]() for which the
nonlinear time is of the same order or less than the linear wave
period and, therefore, we can expect a cut-off of
for which the
nonlinear time is of the same order or less than the linear wave
period and, therefore, we can expect a cut-off of ![]() at
at ![]() . An estimate based on the dynamical equation
(
. An estimate based on the dynamical equation
(![]() ) gives
) gives![]()
![]() . This phenomenological cutoff can be viewed
as a wave breaking process which does not allow wave amplitudes to
exceed their critical value,
. This phenomenological cutoff can be viewed
as a wave breaking process which does not allow wave amplitudes to
exceed their critical value, ![]() for
for ![]() . Now the
normalization condition can be satisfied for the finite-flux
solutions. However, having a constant negative flux
. Now the
normalization condition can be satisfied for the finite-flux
solutions. However, having a constant negative flux ![]() corresponds
to a source at
corresponds
to a source at ![]() which dictates the necessity of a sink for
some
which dictates the necessity of a sink for
some ![]() to preserve the normalization of
to preserve the normalization of ![]() . Note
however that the probability sink does not have to correspond to any
physical ``removal'' of waves with certain amplitudes. The sink should
be present solely because the probability is diluted due to acceptance
of new members with
. Note
however that the probability sink does not have to correspond to any
physical ``removal'' of waves with certain amplitudes. The sink should
be present solely because the probability is diluted due to acceptance
of new members with ![]() into the statistical ensemble. In this
case, the sink must be proportional to the probability and, taking
into account the normalization condition, we can write a modified
equation for the PDF in the presence of cutoff,
into the statistical ensemble. In this
case, the sink must be proportional to the probability and, taking
into account the normalization condition, we can write a modified
equation for the PDF in the presence of cutoff,
Discussion --
We found that the WT intermittency shows as an anomalously high (![]() ) probability of the large-amplitude waves whereas at lower
amplitudes distribution appears to be close to Rayleigh (
) probability of the large-amplitude waves whereas at lower
amplitudes distribution appears to be close to Rayleigh (![]() ) which corresponds to Gaussian wave fields. We showed that
wave breaking is essential for WT intermittency to be present in the
system, yet the details of wave breaking are not important. The role
of wave breaking is just to ensure that no wave can have amplitude
greater than critical value
) which corresponds to Gaussian wave fields. We showed that
wave breaking is essential for WT intermittency to be present in the
system, yet the details of wave breaking are not important. The role
of wave breaking is just to ensure that no wave can have amplitude
greater than critical value ![]() . This simple condition leads to
huge mathematical consequences as it generates the flux solutions in
the amplitude space and therefore creates the
. This simple condition leads to
huge mathematical consequences as it generates the flux solutions in
the amplitude space and therefore creates the ![]() intermittency.
On the other hand, the amplitude of the
intermittency.
On the other hand, the amplitude of the ![]() tail is not prescribed
by WT and will depend on a particular wave breaking mechanisms in a
particular system. However, some conclusions about the dependence of
the tail amplitude on the physical parameters can be reached using a
dimensional arguments.
tail is not prescribed
by WT and will depend on a particular wave breaking mechanisms in a
particular system. However, some conclusions about the dependence of
the tail amplitude on the physical parameters can be reached using a
dimensional arguments.
Consider the classical example of the gravity waves on the surface of
deep water. The linear dispersion relation is given by
![]() , and the coefficient of nonlinear interaction
, and the coefficient of nonlinear interaction
![]() is given in [1]. This system has two power-law steady state
solutions. First one is the spectrum corresponding to the direct
cascade of energy toward high-wave numbers,
is given in [1]. This system has two power-law steady state
solutions. First one is the spectrum corresponding to the direct
cascade of energy toward high-wave numbers,
![]() [1,4]. Second one is the spectrum corresponding to the
inverse cascade of wave action toward the small
[1,4]. Second one is the spectrum corresponding to the
inverse cascade of wave action toward the small ![]() values,
values,
![]() . In addition to the gravity constant
. In addition to the gravity constant ![]() , the
only quantity which determines the state of the system in the direct
cascade range is the energy flux
, the
only quantity which determines the state of the system in the direct
cascade range is the energy flux ![]() whereas in the inverse
cascade range - the particle flux
whereas in the inverse
cascade range - the particle flux ![]() . The PDF tail strength can
be characterized by its area which is a dimensionless number and,
therefore, has to depend on the relevant dimensionless combinations in
the direct and the inverse cascade ranges,
. The PDF tail strength can
be characterized by its area which is a dimensionless number and,
therefore, has to depend on the relevant dimensionless combinations in
the direct and the inverse cascade ranges,
![]() and
and ![]() respectively. Thus, the PDF tail thickness grows
with
respectively. Thus, the PDF tail thickness grows
with ![]() but its length decreases until it completely disappears at
but its length decreases until it completely disappears at ![]() (equal to
(equal to
![]() and
and ![]() respectively).
respectively).
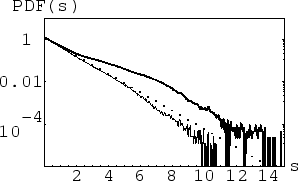
This effect is illustrated in Figure 1 which shows PDF's obtained by
numerical simulations of the dynamical equation for surface gravity
waves on deep water forced at low ![]() 's and dissipated at high
's and dissipated at high
![]() 's. Pseudospectral numerical method similar to that of
[23],[7] was used on a 256x256 grid. Unlike our
study, however, the works in [23],[7] considered
unforced turbulence which was freely decaying and unsteady. Note that
reaching the long-time steadiness was important for us, in order to
accumulate the statistical data necessary for measuring the PDF.
's. Pseudospectral numerical method similar to that of
[23],[7] was used on a 256x256 grid. Unlike our
study, however, the works in [23],[7] considered
unforced turbulence which was freely decaying and unsteady. Note that
reaching the long-time steadiness was important for us, in order to
accumulate the statistical data necessary for measuring the PDF.
At moderate wavenumber (![]() ) one can see a PDF tail in the
range
) one can see a PDF tail in the
range
![]() characterized by an order of magnitude
enhanced probabilities with respect to the Rayleigh distribution.
Unfortunately the range of
characterized by an order of magnitude
enhanced probabilities with respect to the Rayleigh distribution.
Unfortunately the range of ![]() where PDF converged to a stable value
in this experiment was not large enough to reach
where PDF converged to a stable value
in this experiment was not large enough to reach ![]() values and,
therefore, for an asymptotic scaling to develop. To increase this
range a much longer computing to gain good statistics of very rare
events at the PDF tail is necessary, which we can not perform with our
resources.
values and,
therefore, for an asymptotic scaling to develop. To increase this
range a much longer computing to gain good statistics of very rare
events at the PDF tail is necessary, which we can not perform with our
resources.
At a higher wavenumber (![]() ) one can see that the large
amplitude waves are less probable than the ones predicted by the
Rayleigh distribution. This is because the wave breaking happens now
closer to the PDF core causing the PDF cut-off seen at the figure.
) one can see that the large
amplitude waves are less probable than the ones predicted by the
Rayleigh distribution. This is because the wave breaking happens now
closer to the PDF core causing the PDF cut-off seen at the figure.
In this letter we considered WT which is weak on average so that the
wave breaking occurs only in the PDF tail, i.e. ![]() . It
does not apply to the cases when, at some large
. It
does not apply to the cases when, at some large ![]() , the wave breaking
may become so strong that it occurs for most of the waves in the PDF
core. These cases where predicted and discussed in [15], but
their statistics would be hard to describe analytically because of the
strong nonlinearity.
, the wave breaking
may become so strong that it occurs for most of the waves in the PDF
core. These cases where predicted and discussed in [15], but
their statistics would be hard to describe analytically because of the
strong nonlinearity.
Acknowledgments -- Yeontaek Choi's work is supported by KOSEF M07-2003-000-10003-0. YL is supported by NSF CAREER grant DMS 0134955 and by ONR YIP grant N000140210528
 |