Energy spectra of the ocean's internal wave field: theory and observations.
Physical Review Letters 92, 128501 (2004)

Yuri V. Lvov$^1$, Kurt L. Polzin$^2$ and Esteban G. Tabak$^3$,

$^1$ Department of Mathematical Sciences, Rensselaer Polytechnic Institute, Troy NY 12180

91.10.V -

Abstract:

The high-frequency limit of the Garrett and Munk spectrum of internal waves in the ocean and the observed deviations from it are shown to form a pattern consistent with the predictions of wave turbulence theory. In particular, the high frequency limit of the Garrett and Munk spectrum constitutes an exact steady state solution of the corresponding kinetic equation.

Introduction. Internal waves are an important piece of energy and momentum budgets for the earth's atmosphere and ocean. The drag associated with internal wave breaking needs to be included in order to obtain accurate simulations of the atmospheric Jet Stream [1] and it has been argued that the ocean's Meridional Overturning Circulation [2] is forced by the diffusion of mass [3] associated with internal wave breaking [4] rather than by the production of cold, dense water by convection at high latitudes. Both circulations represent important pieces of the earth's climate system.

In a classical work [5], Garrett and Munk demonstrated how observations from various sensor types could be synthesized into a combined wavenumber-frequency spectrum, now called the Garrett-and-Munk (GM) spectrum of internal waves. Consistent only with linear internal wave kinematics, the GM spectrum was developed as an empirical curve fit to available data. Even though deviations have been noted near boundaries [6], and at the equator [7], the last significant model revision [8,9] has surprisingly stood the test of time. However, a review of open ocean data sets reveals subtle variability in spectral power laws. We show in this letter that predictions based upon a weakly nonlinear wave turbulence theory are consistent with both the high frequency-high wave number limit of GM spectrum and the observed variability.

In this letter, we will consider only the high frequency-high wave number limit of GM; for brevity, we shall denote this henceforth as GM$_{h}$. The GM$_{h}$ is given by

$$E(m,\omega) \simeq N m^{-2}\omega^{-2}.$$ (1)

Here $E$ is the spectral wave energy density, $N$ the buoyancy frequency, $m$ the vertical wavenumber, and $\omega$ the frequency. The total energy density of a wavefield is $E=\int E(m,\omega) ~ d m d\omega$.

The possibility that the internal wavefield might exhibit a universal character represents an attractive theoretical target, and much effort (as reviewed by [10]) was devoted to studying the issue of nonlinearity in the context of resonant wave interactions. That line of work is based on a Lagrangian description of the flow, with two main approximations: that fluid particles undergo small displacements, and that nonlinear interactions take place on a much longer time-scale than the underlying linear dynamics. An approximate kinetic equation describing the time evolution of spectral wave energy was derived, and it was shown [11] that the GM$_{h}$ spectrum (1) was close to being a stationary solution.

An alternative to the Lagrangian formulation, based on a Hamiltonian description in isopycnal (density) coordinates, was recently proposed [12]. This approach does not invoke a small-displacement assumption and yields a comparatively simple kinetic equation with an exact steady power-law solution in the high frequency limit. That steady state solution, [see (5) below] is close to the GM$_{h}$ spectrum (1), yet there is a noticeable difference. Motivated by this difference, we tried to estimate the accuracy of the GM$_h$ power laws and thus reviewed extant observations from the literature. In the process of analyzing the data, we found that there was subtle variability in the high wavenumber, high frequency spectrum, forming a distinct pattern.

We then reexamined the kinetic equation of [12] and found its full family of steady state solutions, of which the solution reported in [12] is just one member. This family of solutions compares well with the variability found in the observations. Moreover, the GM$_{h}$ spectrum (1) is a member of this family, thus describing the GM$_{h}$ spectrum simply as an exact steady-state solution to the kinetic equation derived in [12].

Hence, in this article we present evidence for variability in the high frequency-high wavenumber open-ocean internal wavefield, and find that a wave turbulence approach predicts that both GM$_{h}$ itself and the observed variability are stationary states of the kinetic equation. The variability itself, and its likely roots in variable forcing, Coriolis effects, underlying stratification and currents, as well as the low frequency range of the energy spectrum, are fundamental problems posing exciting challenges for future research.

Overview of observations: a family of spectra. Below we present a summary of historical oceanic internal wave energy spectra. These observations are re-analyzed to study whether the high-frequency, high-wavenumber spectra may form a pattern. We review seven data sets available in the literature. We shall present a detailed analysis of these data sets elsewhere; here we just list them along with their high-frequency, high-wave number asymptotics. Let us assume that, in this limit, the three dimensional wave action $n({\bf k},m)$ can be approximated by horizontally isotropic power laws of the form

$$n_{{\bf k},m}= n_0 \ \vert{\bf k}\vert^{-x} \vert m\vert^{-y} \, ,$$ (2)

where ${\bf k}$ is the horizontal wave vector, $k=\vert{\bf k}\vert$ its modulus, $m$ vertical wavenumber and $n_0$ is a constant.

Using the linear dispersion relation of internal waves, $\omega_{{\bf k},m}\propto \vert{\bf k}\vert/m$, this action spectrum can be transformed from the wavenumber space $(k,m)$ to the vertical wave-number-frequency space $(\omega,m)$ . Multiplication by the frequency yields the corresponding energy spectrum,

$$E(m,\omega)\propto \omega^{2-x} m^{2-x-y} ~~ .$$

The total energy of the wave field is then

$$E=\int \omega({\bf k},m) n({\bf k},m)\ d{\bf k} d m = \int E(\omega,m) \ d\omega d m .$$

Below we list extant data sets with concurrent vertical profile and current meter observations and some major experiments utilizing moored arrays, along with our best estimate of their high-wave-number high frequency asymptotics (the order is chronological):
$\bullet$ The Mid-Ocean Dynamics Experiment (MODE), March-July 1973, Sargasso Sea ( $26^{\circ} 0^{\prime}$ N, $69^{\circ} 40^{\prime}$ W): $m^{-2.25}\omega^{-1.6}$ [13];
$\bullet$ The Internal Wave Experiment (IWEX), 40 days observations in November-December 1973, Sargasso Sea thermocline ( $27^{\circ} 44^{\prime}$ N, $69^{\circ} 51^{\prime}$ W): $k^{-2.4 \pm 0.4}\omega^{-1.75}$  [14];
$\bullet$ The Arctic Internal Wave Experiment (AIWEX), March to May of 1985, Canada Basin thermocline, ($74^{\circ}$ N, $143-146^{\circ}$ W): $m^{-2.15}\omega^{-1.2}$ [15,16];
$\bullet$ The Frontal Air-Sea Interaction Experiment (FASINEX), January to June of 1986, Sargasso Sea thermocline ($27^{\circ}$ N, $70^{\circ}$ W): $m^{-1.9~{\rm to}~-2.0}\omega^{-1.75}$ [17,18];
$\bullet$ Patches Experiment (PATCHEX), 7.5 days during October of 1986, eastern Subtropical North Pacific, ($34^{\circ}$ N, $127^{\circ}$ W): $m^{-1.75}\omega^{-1.65~{\rm to}~-2.0}$ [19];
$\bullet$ The Surface Wave Process Program (SWAPP) experiment, 12 days during March, 1990, eastern Subtropical North Pacific thermocline, ($35^{\circ}$ N, $127^{\circ}$ W): $m^{-1.9}\omega^{-2.0}$ [20];
$\bullet$ North Atlantic Tracer Release Experiment (NATRE), February-October 1992, eastern Subtropical North Atlantic thermocline, ($26^{\circ}$ N $29^{\circ}$ W): $m^{-2.75}\omega^{-0.6}$ (for $1 < \omega < 6$cpd) [21].
These deep ocean observations (Figure 1) exhibit a higher degree of variability than one might anticipate for a universal spectrum. Moreover, the deviations from the GM$_{h}$ spectral power laws form a pattern: they seem to roughly fall upon a curve with negative slope in the $(x,y)$ plane. We show in the next section that the predictions of wave turbulence theory are consistent with this pattern.

A wave turbulence formulation for the internal wave field. In this section we assume that the internal wave field can be viewed as a field of weakly interacting waves, thus falling into the class of systems describable by wave turbulence. Wave turbulence is a universal statistical theory for the description of an ensemble of weakly interacting particles, or waves. This theory has contributed to our understanding of spectral energy transfer in complex systems [22], and has been used for describing surface water waves since pioneering works by Hasselmann [23], Benney and Newell [24] and Zakharov [25,26].

The dynamics of oceanic internal waves can be most easily described in isopycnal (i.e. density) coordinates, which allow for a simple and intuitive Hamiltonian description [12]. To describe the wave field, we introduce two variables: a velocity potential $\phi({\bf r},\rho)$, and an isopycnal straining $\Pi({\bf r},\rho)$. The horizontal velocity is given by the isopycnal gradient $\nabla$ of the velocity potential, ${u({\bf r},\rho) =\nabla \phi({\bf r},\rho)}$. The straining $\Pi =\rho/(\partial_z\rho)$ can also be interpreted as the fluid density in isopycnal coordinates.

These two variables form a canonically conjugated Hamiltonian pair, so that the primitive equations of motion (i.e. conservation of horizontal momentum, hydrostatic balance, mass conservation and the incompressibility constraint) can be written as a pair of canonical Hamilton's equations,

$$\partial_t \Pi=\delta {\cal H}/\delta \phi, \ \ \ \ \ \ \ \partial_t \phi=-\delta {\cal H}/\delta \Pi \, ,$$

$${\cal H} = \frac{1}{2}\int \left( \Pi \, \vert\nabla \phi\vert^2 ... ...t^{\rho} \frac{\Pi}{\rho_1} \, d\rho_1\right\vert^2 \right) d {\bf r} d \rho\,.$$

The first term in the Hamiltonian clearly corresponds to the kinetic energy of the flow, the second term can be shown to correspond analogously to the potential energy.

Performing the Fourier transform, and introducing a complex field variable $a_{\bf p}$ via

$$\phi_{\bf { p}}=\frac{i N \sqrt{\omega_{\bf { p}}}}{\sqrt{2 ... ...}}N}\left(a_{\bf { p}}+a^*_{-{\bf { p}}}\right)\, , \nonumber$$

where ${\bf p}=({\bf k},m)$ is the 3-d wave vector, $N$ is buoyancy frequency, $g$ is gravity acceleration; the canonical pair of equations of motion and the Hamiltonian (3) read

$$i\frac{\partial}{\partial t} a_{{\bf { p}}} = \frac{\partial {\ca... ...cal H}=\int \omega_{\bf { p}}\, \vert a_{{\bf { p}}}\vert^2 \, d {{\bf { p}}} +$$

$$\int V_{ {{\bf { p_1}}} {{\bf { p_2}}} }^{{\bf { p_3}}} \left( a_... ...\bf { p_2}}} - {{\bf { p_3}}}} \, d{{\bf { p_1}}d {\bf { p_2}}d {\bf { p_3}}} +$$

$$\int \frac{1}{6}V_{ {{\bf { p_1}}} {{\bf { p_2}}}}^ {{\bf { p_3}}... ...+ {{\bf { p_2}}} +{{\bf { p_3}}}}\, d {\bf { p_1}}d {\bf { p_2}}d {\bf { p_3}},$$

with wave-wave interaction matrix elements given by [12]: $V^{{\bf { p}}}_{{\bf { p_1}}{\bf { p_2}}}= U^{{\bf { p}}}_{{\bf { p_1}}{\bf { p... ...\bf { p_1}}}_{{\bf { p}}{\bf { p_2}}}+U^{{\bf { p_2}}}_{{\bf { p}}{\bf { p_1}}}$ with

$$U^{{\bf { p}}}_{{\bf { p_1}}{\bf { p_2}}}= - \frac{N}{4\sqrt... ...\bf { p_2}}} \omega_{\bf { p_3}}}{\omega_{\bf { p_1}}}} k_1 ~.$$

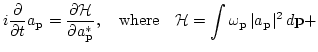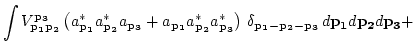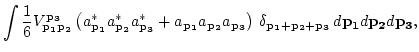These field equations are equivalent to the primitive equations of motion for internal waves (up to the hydrostatic balance and Boussinesq approximation); the work reviewed in [10] instead resorted to a small displacement approximation to arrive at similar equations. We will argue elsewhere that this extra assumption does not provide an internally consistent description of interactions between extremely scale separated waves. For the purposes of this letter, it suffices to note that the two kinetic equations are different and yield different steady solutions.

We shall characterize the field of interacting internal waves by its wave action $\delta_{{\bf p} - { \bf p'}} n_{\bf p} = \langle a_{\bf p} a^*_{\bf p'} \rangle.$

Under the assumption of weak nonlinear interaction, one derives a closed equation for the evolution of the wave action, the kinetic equation. Assuming horizontal isotropy, the kinetic equation can be reduced further by averaging over all horizontal angles, obtaining [with $p=(k,m)$ and $d p_1 d p_2 = d k_1 d m_1 d k_2 d m_2$]

$$\frac{d n_{k,m}}{d t} = \frac{1}{k}\int \left(R^p_{p_1 p_2}-R^{p_1}_{p p_2}-R^{p_2}_{p_1 p}\right) d p_1 d p_2 /\Delta^k_{k_1 k_2},$$

$$R^p_{p_1 p_2}= \delta_{\omega_{p}-\omega_{p_1}-\omega_{p_2}} \, f^p_{p_1 p_2} \, \vert V^p_{p_1 p_2}\vert^2 \, \delta_{m-m_1-m_2} k k_1 k_2 \, ,$$

where $f^p_{p_1 p_2} = n_{p_1}n_{p_2} - n_{p}(n_{p_1}+n_{p_2}) \$ and $\Delta^k _{k_1 k_2} = \Big( 2 \left[ (k k_1)^2 +(k k_2)^2 +(k_1 k_2)^2 \right]-k^4-k_1^4 -k_2^4\Big)^{1/2}/2$.

A family of steady state power-law solutions to the kinetic equation. In wave turbulence theory, three-wave kinetic equations admit two classes of exact stationary solutions: thermodynamic equilibrium and Kolmogorov flux solutions, with the latter corresponding to a direct cascade of energy -or other conserved quantities- toward the higher modes. The fact that the thermodynamic equilibrium -or equipartition of energy- $n_{\bf p} = 1/\omega_{\bf p}$ is a stationary solution of (4) can be seen by inspection, whereas in order to find Kolmogorov spectra one needs to be more elaborate. In [12] we used the Zakharov-Kuznetsov conformal mapping [25,26,27] to show analytically that the following wave action spectrum constitutes an exact steady state solution of (4) [note the difference with (1)]:

$$n_{{\bf k},m}= n_0\ \vert{\bf k}\vert^{-7/2} \vert m\vert^{-1/2};\ E(m,\omega) \propto \omega^{-1.5}m^{-2},$$ (3)

Remarkably though, this is not the only steady state solution of the kinetic equation having nonzero spectral energy fluxes. In fact, there is a full family of such power law steady solutions. To see this, consider the kinetic equation (4), and substitute into it the ansatz (2). Let us now denote the resulting RHS of (4) by $I(k,m)$. For steady states, $I(k,m)$ needs to vanish for all values of $k$ and $m$, for appropriately chosen values of $(x,y)$. However, once $I$ vanishes for one such wavenumber $(k,m)$, it does so for all, due to the fact that $I$ is a bi-homogeneous function of $k$ and $m$:

$$I( \alpha k ,\beta m) = \alpha^{4 + 2 x} \beta^{1 + 2 y} I( k, m).$$ (4)

Hence we can fix $k$ and $m$, and seek zeros of $I$ as a function of $x$ and $y$. The exact analytical solution (5) cannot correspond to an isolated zero of $I$, since $(\partial_x I,\partial_y I)$ is nonzero (it is proportional to the energy flux in the Kolmogorov solution [22]). Hence, by the Implicit Function Theorem, there must exist a curve of zeros of $I(x,y)$.

Since this family of steady state solutions is not all apparently amenable to a closed form, we sought the zeros of $I$ by numerical integration. This involves a certain amount of work. First, the delta-functions in (4) restrict contributions to the resonant set. Consider, for example, the resonant set

$${\bf k} = {\bf k_1} + {\bf k_2}, \ {m} = { m_1} + { m_2},\ \omega_{k,m} = \omega_{k_1,m_1} + \omega_{k_2,m_2}.$$

Given $\bf k$, $\bf k_1$, $\bf k_2$ and $m$, one can find $m_1$ and $m_2$ satisfying this resonant condition by solving

$${k}/{m}={k_1}/{\vert m_1\vert} +{k_2}/{\vert m-m_1\vert}.$$

This equation reduces to a quadratic equation for $m_1$, and then one can find $m_2$ from $m_2=m-m_1$. After this reduction, one is left with a two-dimensional integral, over $\vert k_1\vert$ and $\vert k_2\vert$. This infinite domain is further restricted by the requirement that $\vert k_1\vert$, $\vert k_2\vert$ and $\vert k\vert$ are such that they can correspond to the sides of a triangle; this restricted (though still infinite) domain is called the kinematic box in the oceanographic literature. The next problem for the numerical integration is that the integrand diverges ( typically in an integrable fashion) at the boundaries of the domain. This is solved by a suitable change of variables. Finally, a second substitution renders the domain of integration finite.

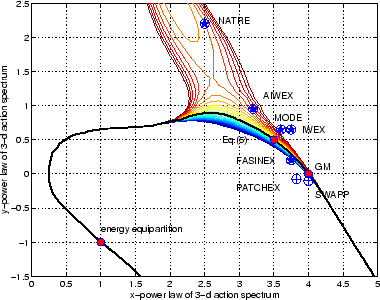
The resulting family of zeros is depicted in Figure 1. Notice that the curve passes through the exact solution (5). More importantly, it also passes through the point $(4,0)$, corresponding to the GM$_{h}$ spectrum (1). Hence this classical spectrum is for the first time shown to correspond to an exact steady solution to a kinetic equation based on first fluid principles.

Finally, we note the integrals converge in the parameter regime occupied by the observations. In regions of tightly spaced contour lines ($x < 1.7$ and $y< 0.7$, $x > 4.2$ and $y < -0.4$) (4) is nonintegrable.

The other points marked on the figure correspond to the observational sets discussed above. Notice that, with the exception of NATRE, they all lie very close to the zeros of $I$. Therefore the predictions of wave turbulence are consistent with the observed deviations from GM$_{h}$.

In fact, the NATRE point lies in an area of $(x,y)$ space where $z=I$ and $z=0$ are nearly tangential, thus making the line of zeros effectively ``thicker'' (in other words, the collision integral is not zero at the observed points, but it is very small, possibly allowing other, typically smaller effects to take over.)

- Conclusions We have shown that the wave turbulence formalism captures much of the variability apparent in the oceanic internal wave field. This includes the characterization of the spectral curve put together by Garrett and Munk as an exact steady solution to a kinetic equation for the evolution of the wave field, derived from first principles. In addition, the curve of steady solutions to this kinetic equation is consistent with much of the observed variability in the energy spectra. We conjecture that the placement along this curve of individual observations depends on the nature of the forcing (for instance, by tides and atmospheric winds), the local degree of stratification, vorticity and shear, and the variable magnitude of the Coriolis parameter. This is the subject of ongoing research.

Acknowledgments YL is supported by NSF CAREER grant DMS 0134955 and by ONR YIP grant N000140210528; KP is supported by NSF grant OCE 9906731; ET is supported by NSF grant DMS 0306729.

Figure: Ocean observations and analytical zeroes of the kinetic equation (4) in the $(x,y)$ plane, with the high-frequency action spectrum given by the power law (2). Solid red dots represent the thermodynamical equilibrium solution, the closed-form zero (5) and the GM$_{h}$ spectrum (1). Blue circles represent different observational sets. The solid black curve marks the numerically computed zeros of the kinetic equation. Contour lines of the RHS of the equation (4) with high-frequency action spectrum given by the power law (2), $I(x,y)$, are also shown, with red curves correspond to positive values, and blue to negative values.