Yuri V. Lvov[]
Esteban G.Tabak []
Yuri V. Lvov[]
[]
Department of Mathematical Sciences, Rensselaer Polytechnic Institute,
Troy, NY 12180
[]
Courant Institute of Mathematical Sciences,
New York University, New York, NY 10012.
This paper first appeared at PRL Vol 87, page 168501, 2001
and contained some misprints corrected below
Esteban G.Tabak []
Introduction.-- Remarkably, the internal wave spectrum in the
deep ocean has much the same shape wherever it is observed, except
when the observations are made close to a strong source of internal
waves [1]. This observation led Garrett and Munk
[2,3,4] to propose an analytical form of the internal
wave spectrum that approximates many observations. This spectrum is
now called the Garrett-Munk (GM) spectra of internal waves. The total
energy of the internal waves may be represented as an integral over
spectral energy density![]()
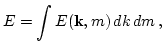 |
(1) |
The dispersion relation underlying this proposed spectrum is that
of long internal waves, with a profile rapidly oscillating in the vertical,
so that both the hydrostatic balance and the WKB approximation apply:
The GM spectrum constitutes an invaluable tool for oceanographers, assimilating hundreds of different observations into a single, simple formula, that clarifies the distribution of the energy contents of internal waves among spatial and temporal scales. Yet a number of questions regarding the spectrum itself remain open. One is about its accuracy: Garrett and Munk basically made up a family of spectra, depending on a few parameters, that was simple and consistent with the dispersion relation (3) for long internal waves; and then fitted the parameters to match observational data. Their success speaks of their powerful intuition, yet it leaves the door open to question both the accuracy of the parameter fit, and the appropriateness of the proposed family of spectra, necessarily incomplete, which involved a high degree of arbitrariness. The other question, more fundamental to theorists, is to explain or derive the form of the spectrum from first principles. Such explanation should surely involve the nonlinear interaction among internal modes, as well as the nature of the forcing and dissipation acting on the system.
In this work, we elucidate which spectrum the theory of wave turbulence (WT) would predict for internal waves in scales far away from both the forcing and the dissipation. Wave turbulence theory (also called weak turbulence, to contrast it to the ``strong'' turbulence of isotropic fluids) applies to Hamiltonian systems characterized by a scale separation between a fast, linear dispersive wave structure, and its slow, nonlinear modulation.
In what follows we assume that there is pumping of energy into the internal wave field by the wind, by interaction with surface waves, or by other processes. We assume that these pumping processes can be characterized by wavelengths of the order of hundreds of meters. Moreover, we assume that the processes which remove energy from the internal wave field, such as wave breaking, turbulent mixing, multiple reflections from the surface and bottom boundary layers, or interaction with bottom topography, can be characterized by lengthscales of less than a meter. Then there is a region of lengthscales, called inertial interval or transparency region, where dissipation and pumping processes are not important. It is the nonlinear wave interaction which determines the form of the spectrum in the region of transparency. Energy then gets into the system of internal waves at large scales, cascades through the inertial scales via multiple nonlinear interactions, and is absorbed in the small scales by the dissipation processes. This scenario corresponds to the Kolmogorov spectrum of WT theory [5]. According to WT, the energy distribution in the inertial region is defined solely by the nature of nonlinear interactions and by the linear dispersion relation of the waves in the system.
Notice that, in the transparency region, the dispersion relation
is self-similar, since ![]() . When this is the case,
and the nonlinearity is homogeneous, WT theory predicts
self-similar stationary solutions.
For
. When this is the case,
and the nonlinearity is homogeneous, WT theory predicts
self-similar stationary solutions.
For ![]() and
and ![]() , the Garrett-Munk spectrum
(2) becomes
, the Garrett-Munk spectrum
(2) becomes
Hamiltonian structure and kinetic equation--
The equations for long internal waves in an incompressible
stratified fluid are
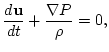 |
|||
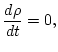 |
Changing to isopicnal coordinates, where the roles of the vertical
coordinate ![]() and the density
and the density ![]() as independent and dependent
variables are reversed, the equations become:
as independent and dependent
variables are reversed, the equations become:
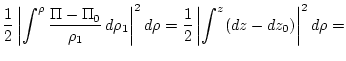 |
|||
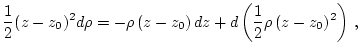 |
(10) |
For simplicity, we shall take the buoyancy frequency ![]() of the
equilibrium profile to be a constant, and we shall replace the
density
of the
equilibrium profile to be a constant, and we shall replace the
density ![]() in the denominator of the Hamiltonian's potential
energy by a constant
in the denominator of the Hamiltonian's potential
energy by a constant ![]() . This is the WKB -also Boussinesq-
approximation, which makes sense for waves varying rapidly in the
vertical direction, particularly since the water density
typically changes only by a few percent over the full depth of
the ocean.
. This is the WKB -also Boussinesq-
approximation, which makes sense for waves varying rapidly in the
vertical direction, particularly since the water density
typically changes only by a few percent over the full depth of
the ocean.
Let us decompose ![]() into the
sum of its equilibrium value and deviation from equilibrium
into the
sum of its equilibrium value and deviation from equilibrium
![]() Since, in the WKB limit, the linear part of the resulting Hamiltonian
has constant coefficients, it is natural to perform a Fourier
transformation in both vertical and horizontal directions. We assume
that both Fourier spectra are continuous, which is a reasonable
approximation if the wave's vertical wavelengths are much smaller
than the depth of the ocean.
Then
Since, in the WKB limit, the linear part of the resulting Hamiltonian
has constant coefficients, it is natural to perform a Fourier
transformation in both vertical and horizontal directions. We assume
that both Fourier spectra are continuous, which is a reasonable
approximation if the wave's vertical wavelengths are much smaller
than the depth of the ocean.
Then
We now introduce a canonical transformation which transfers the
equations of motion for the Fourier components ![]() and
and ![]() into a single equation for the canonical
variable
into a single equation for the canonical
variable ![]() . We choose this transformation
so that the quadratic part of Hamiltonian becomes diagonal in
. We choose this transformation
so that the quadratic part of Hamiltonian becomes diagonal in
![]() . The canonical transformation reads:
. The canonical transformation reads:
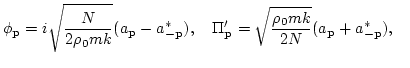 |
| (12) |
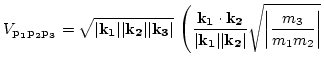 |
|||
 |
The form of this Hamiltonian is typical for systems with
three-wave interactions and cylindrical symmetry. Following
wave turbulence theory, one proposes a perturbation expansion
in the amplitude of the nonlinearity.
To zeroth order in the perturbation, one recovers the linear waves.
At higher orders, the nonlinear interactions lead to a slow modulation
of the wave amplitudes, representing spectral
transfer of the conserved quantities of the Hamiltonian.
This transfer manifests itself in the perturbation expansion through resonances or secular terms, occurring on the
so called resonant manifold. Energy transfer is described by an
approximate kinetic equation for the ``number of waves'' or wave-action
![]() , defined by
, defined by
Assuming horizontal isotropy, one can average
(15) over all horizontal angles, obtaining
In wave turbulence theory, three-wave kinetic equations admit two classes
of exact stationary solutions: thermodynamic equilibrium and
Kolmogorov flux solutions, with the latter
corresponding to a direct cascade of energy
-or other conserved quantities- toward the higher modes.
The fact that the thermodynamic equilibrium -or equipartition of energy-
![]() is a stationary solution of
(16) can be seen by
inspection, whereas in order to find Kolmogorov spectra one needs to
be more elaborate. Let us assume that
is a stationary solution of
(16) can be seen by
inspection, whereas in order to find Kolmogorov spectra one needs to
be more elaborate. Let us assume that ![]() is given by
the power-law anisotropic distribution
is given by
the power-law anisotropic distribution
| (17) | |||
This is the main result of this article - the short wave part of the Garrett-Munk spectra is close to the stationary solution to a kinetic equation hereby derived for internal waves, based on a Hamiltonian structure appearing naturally in isopicnal coordinates.
A modified Garrett-Munk spectrum--
In this section, we show how a minor modification of the
Munk-Garrett formalism allows us to match the wave turbulence
prediction (6). As in [3], we introduce two functions
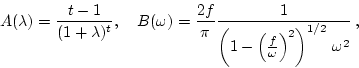
| (18) |
Then, following [3], we propose an energy spectrum
of the form
Conclusion.-- We have found a natural Hamiltonian formulation
for long internal waves, and used it within the wave turbulence
formalism to determine the stationary energy spectrum corresponding to
a direct cascade of energy from the long to the short waves. This
spectrum is close to the one that Garrett and Munk fitted to available
observational data. The small difference could be due either to
physical effects that the wave turbulence formalism fails to capture,
or to a real necessary correction to the GM spectrum. We show how a
slight modification of the GM spectrum yields results in agreement
with WT theory.